停留1分钟，助你上重高！动点最值视频精讲，赠配套纸质教材。

承接上一期视频，再把这道江苏的模考的压轴题的第二种解法给大家分享一下。

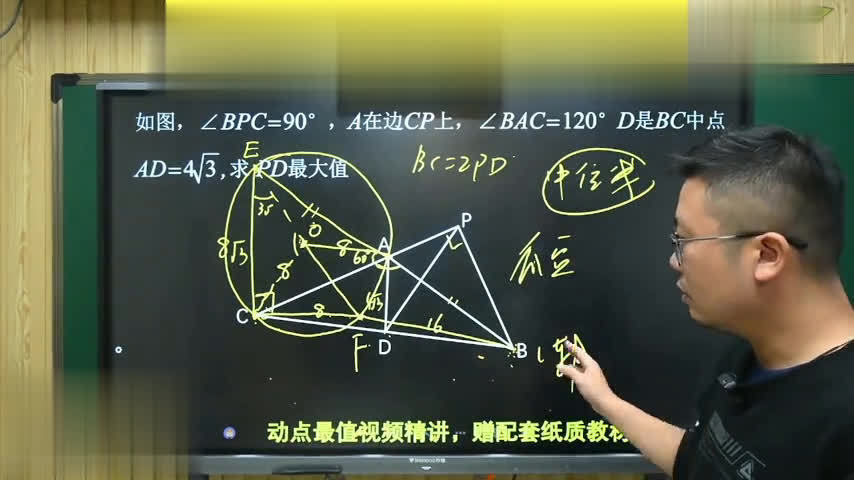
把这道题图形往下拖了一点，这里面仍然简单的说一下这个条件，它是一个直角三角形，d点是bc边上的终点，a点在bc这条边上面运动。现在ad的长度等于四倍杠三，是一个定值，这个角是一百二十度的角。现在同样还让我们去计算pd的最大值。

对于这道题，刚刚之前分享的那种方法是利用终点来构造背长，把不在一个三角形里面的定角和定边放在一个三角形里面。这道题的第二种解法同样还是这个思路，只是现在把终点不变成它的背长，变成什么？变成中微线。不管是中微线还是背长，都是这个课程里面非常重要的所要讲的技巧。

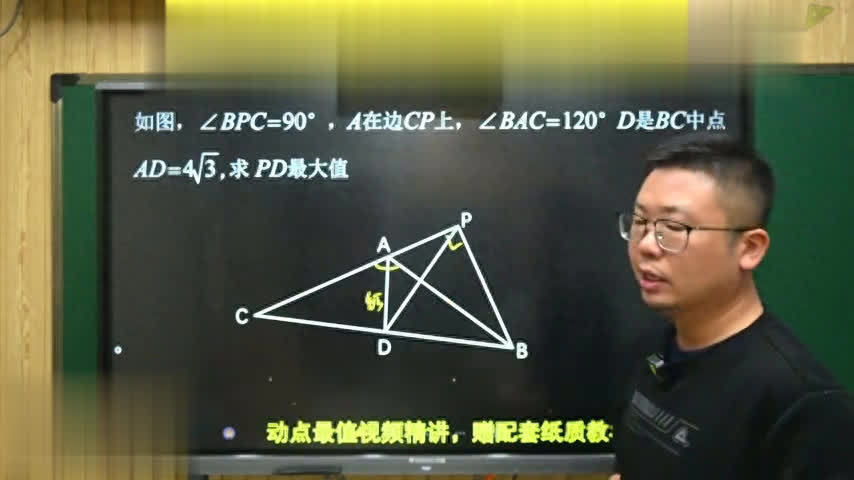
怎样去变成中微线？把b a这条边进行延长，再把这两个点连接起来，延长到e点位置，使ae的长度和ab相等，这样一百二十度的零补角就是一个六十度的角得到了。并且第一点是bc的终点，此时ad就相当于bce三角形的一条中微线。

既然是中微线，底边是这条中微线的两倍，所以它就是八倍的根号三。由此是不是也获得了一个固定的边对应一个固定的角？此时仍然是可以把ace三角形的外接圆做出来，圆心角大概在这个位置，把它俩连接起来，这个圆具体就不画了，画一下，还是画一下，这个是圆心，大概画一下就这样的情况。

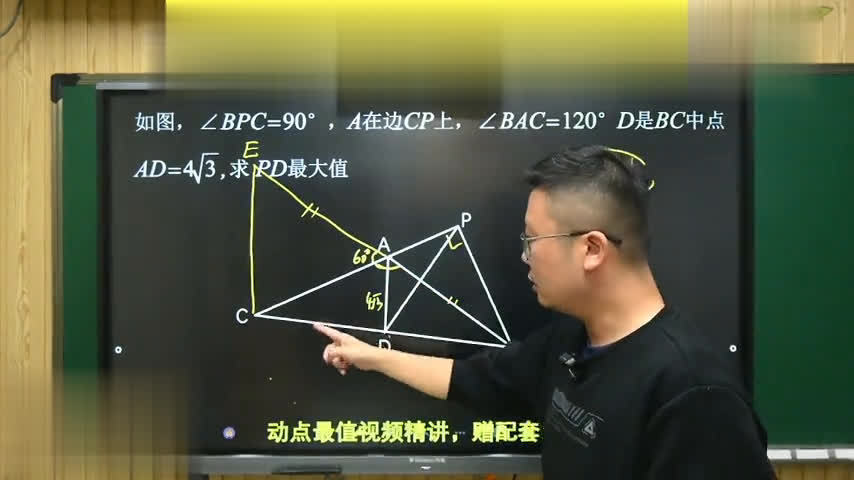
这样画出来以后有同学说后面怎么办？后面问题其实可以把它理解成什么？这个刮斗模型的情况叫直线型刮斗，比较简单的一种方式。刚刚说的这里面可以把c点看到是一个定点，因为这条边是一个固定的边，把它看成一个定点，要求pd的最大值其实就是要求bc的最大值，因为bc正好是两倍的pd，只要在斜边上中线等于斜边的一半，所以如果是定点就看一下b点的轨迹不就行了吗？

b点怎样去运动的？因为a点正好在这个圆上面运动，a的正好又是bb的终点，也可以看到是一个固定的点，所以根据刮豆模型也可以迅速的找到b点的轨迹，也是一个什么？也是一个圆。

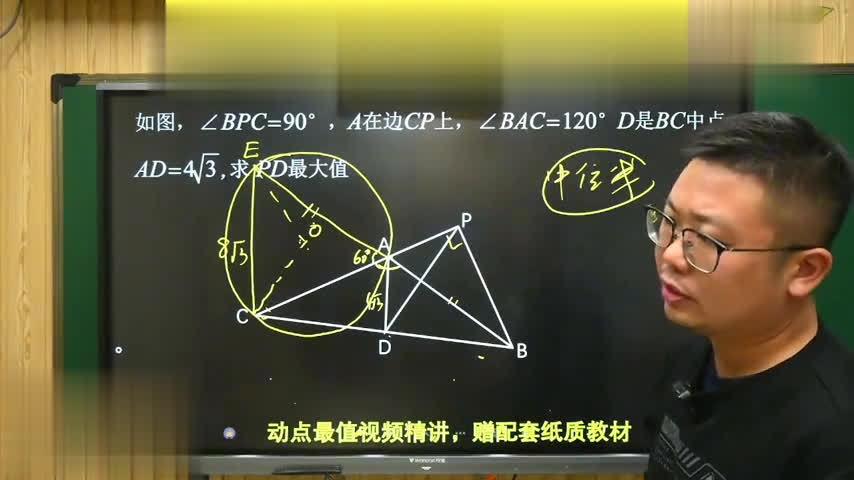
它的半径在什么地方？它的圆心在什么地方？可以怎么办？可以把这个点进行延长，和它仍然有个交点。这个点用f点来表示，因为f点和e点的终点是不是圆心o点，b点、e点的圆心终点是不是a点。

也就是说此时如果把oa连接起来，再把这里面的fb连接起来，大家看一下oa是一个定长，等于几？等于八，它的长度也被八。这个外结缘为什么等于八？因为上一个讲过了，它是一百二十度，这条边是八倍矿山，所以这条边正好多少？八，半径就是八。

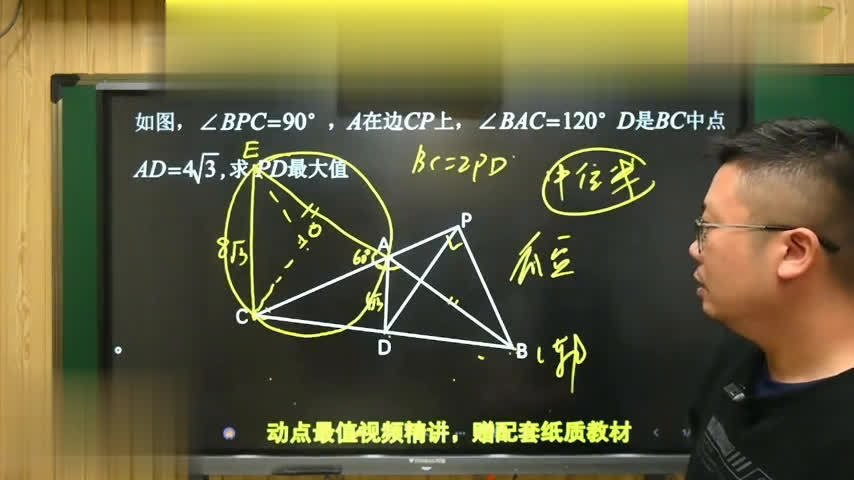
然后看一下fb的中位线是不是正好是它？所以fb的长度等于多少？等于十六，这条边是一个固定的边。现在要求bc的最大值，其实再把它俩连接起来，这个位置可以根据原来处理，这个点实际上是一个固定的点。

为什么是一个固定的点？因为刚刚说的这个角是一个三十度的角，这个角也是一个三十度的角，把它延长以后和它有交点，这是直径，所以这个角必然是一个直角。这条边的长度正好是直径的一半，多少？也是八。

大家看看是不是？也就是cf长度是个固定的值，fb的长度也是个固定的值。bc的长度在这个三角形里面，可以利用什么？可以利用三角形的三边关系，不去考虑它的轨迹，也可以直接就是bc必然是小于或者等于两边之和多少？二十四。

bc的一半正好就是f，就是p、d，它的最大值就是它的一半等于多少？等于十二。这道题就搞定了。同样可以怎么样利用圆的姿势去轨迹的方式？因为这个点是一个定点，这条边的长是一个定长，所以b点的轨迹完全可以看到是以它的圆心，以它为圆心，以它的一半为半径这样的一个圆上面运动。

这个圆比较大，具体就画一下，现在在圆心上找一点，使它到c点的距离是最长的，怎么找？肯定是连接c点和圆心所在的位置再延长一下和它有个交点，这个长度始终是个固定的是十六，这条边是八，所以它俩的和多少？二十四。这样b点在这个位置，c、b的长度最大值就是多少？二十四。

所以问题其实虽然是两个不同的东西，完全可以把它放在一起去加以理解。这类问题想要站的更高，可以了解一下这个课程，学完以后我相信你对它其实对你来说是你的一个得分点，并不是你的一个丢分点。